如何对齐不同初始化大小下的 Data scaling 曲线

现象

我们在 上一篇 blog 中讨论了 scaling law 到底是如何产生的。我们在其预印本中增加了实验章节，其中有一系列图展示了不同 $\alpha$ 下的 data scaling 曲线，比如其中一张图，展示了在数据受限的情况下，loss 与 datasize 的关系

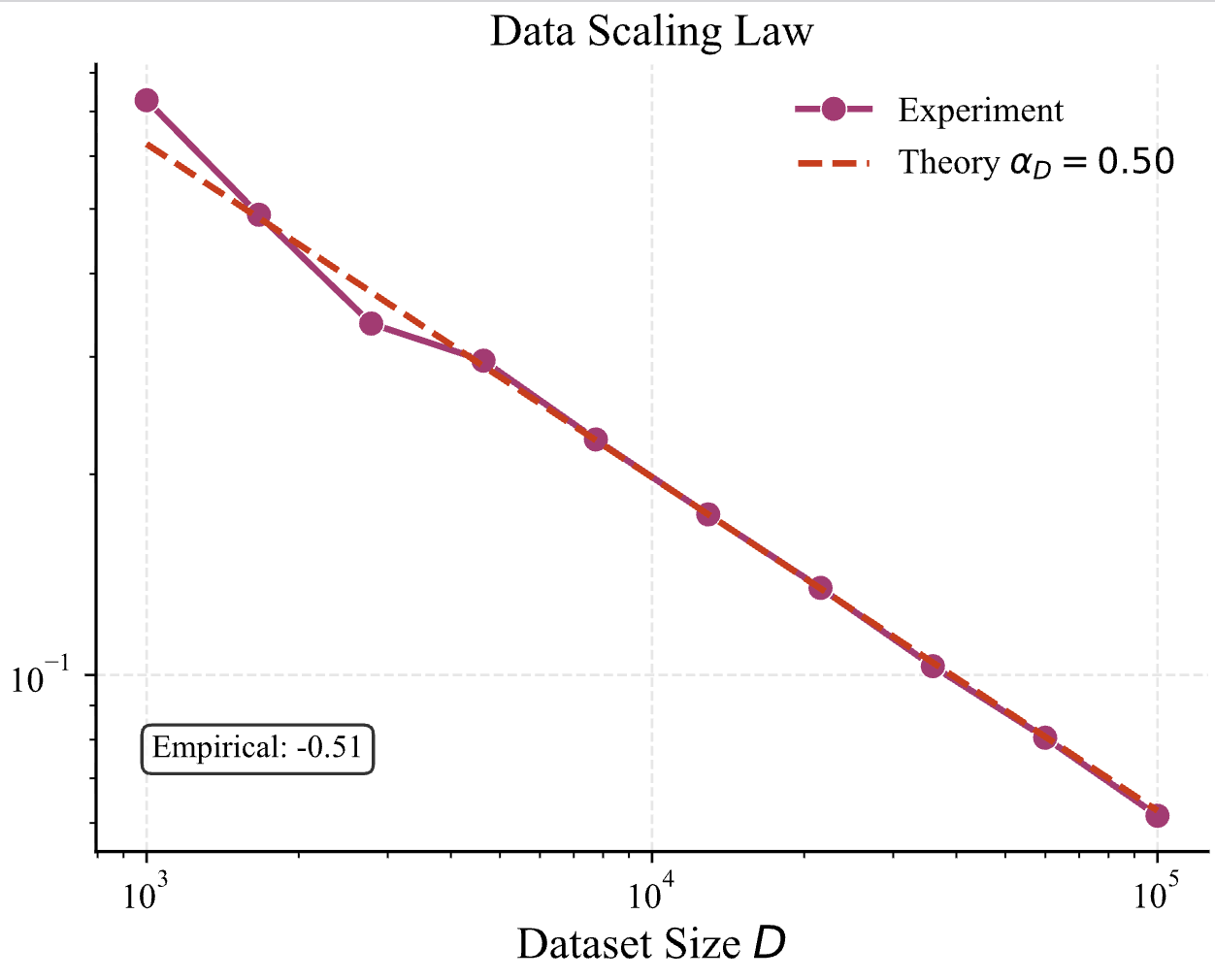
为了确保发生 feature learning，在这张图里，我们设定初始化的 std=0.01。但是如果我们把 std 增大一些，设置成 0.05，会发生什么呢？结果如下

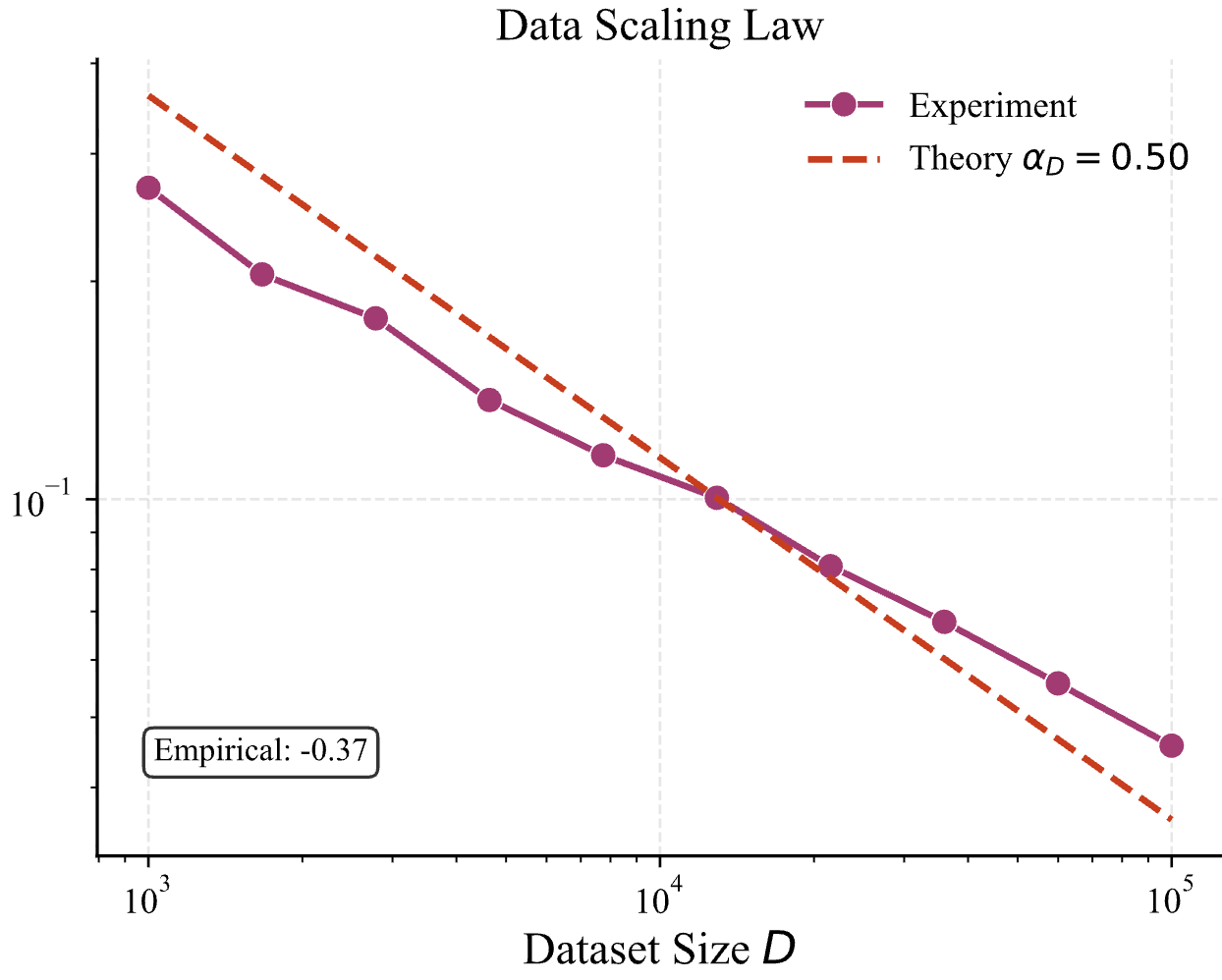
我们可以看见，std=0.05 时，data scaling 的曲线发生了偏移，那如果再增大一些呢？设置成 0.1，结果如下

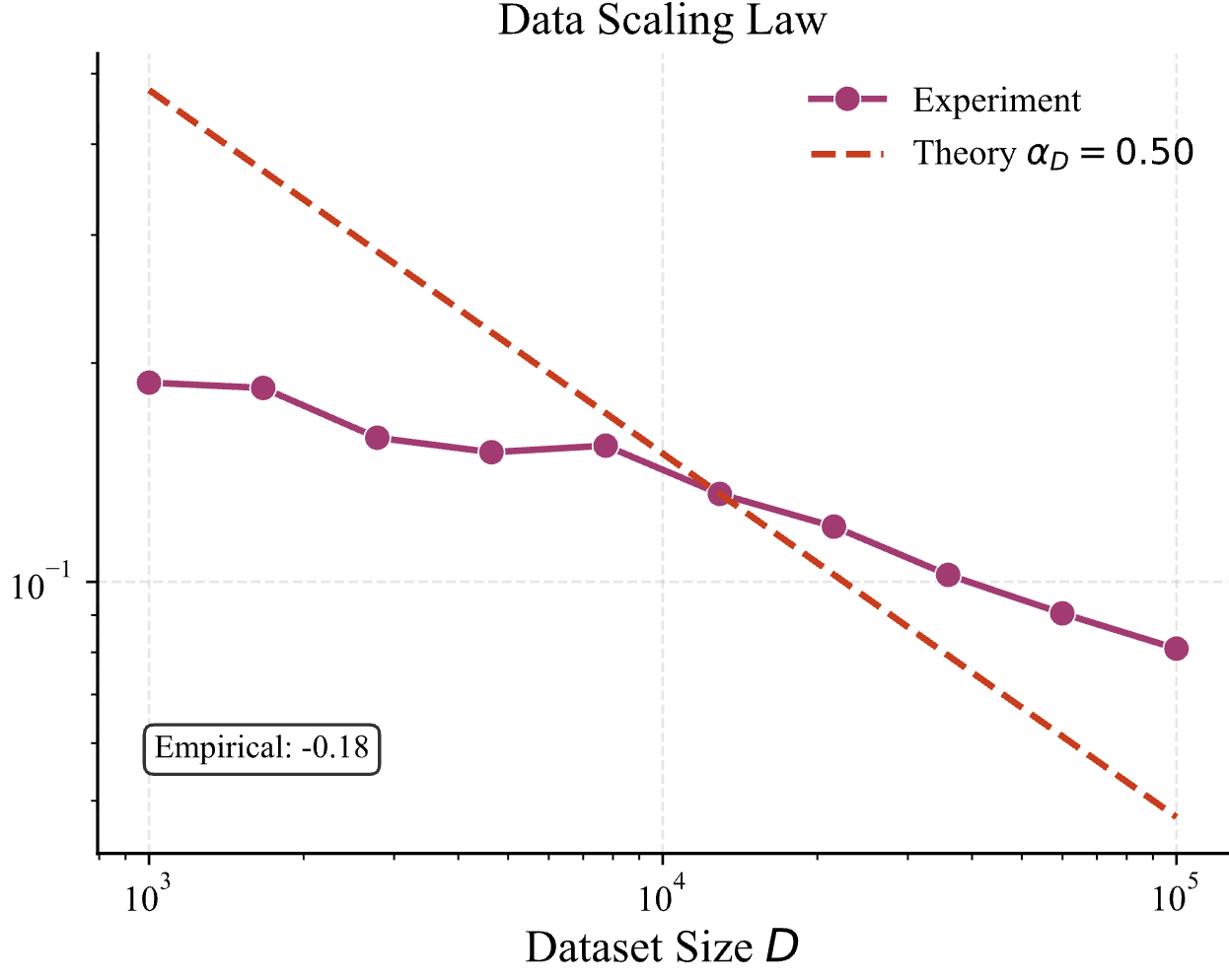
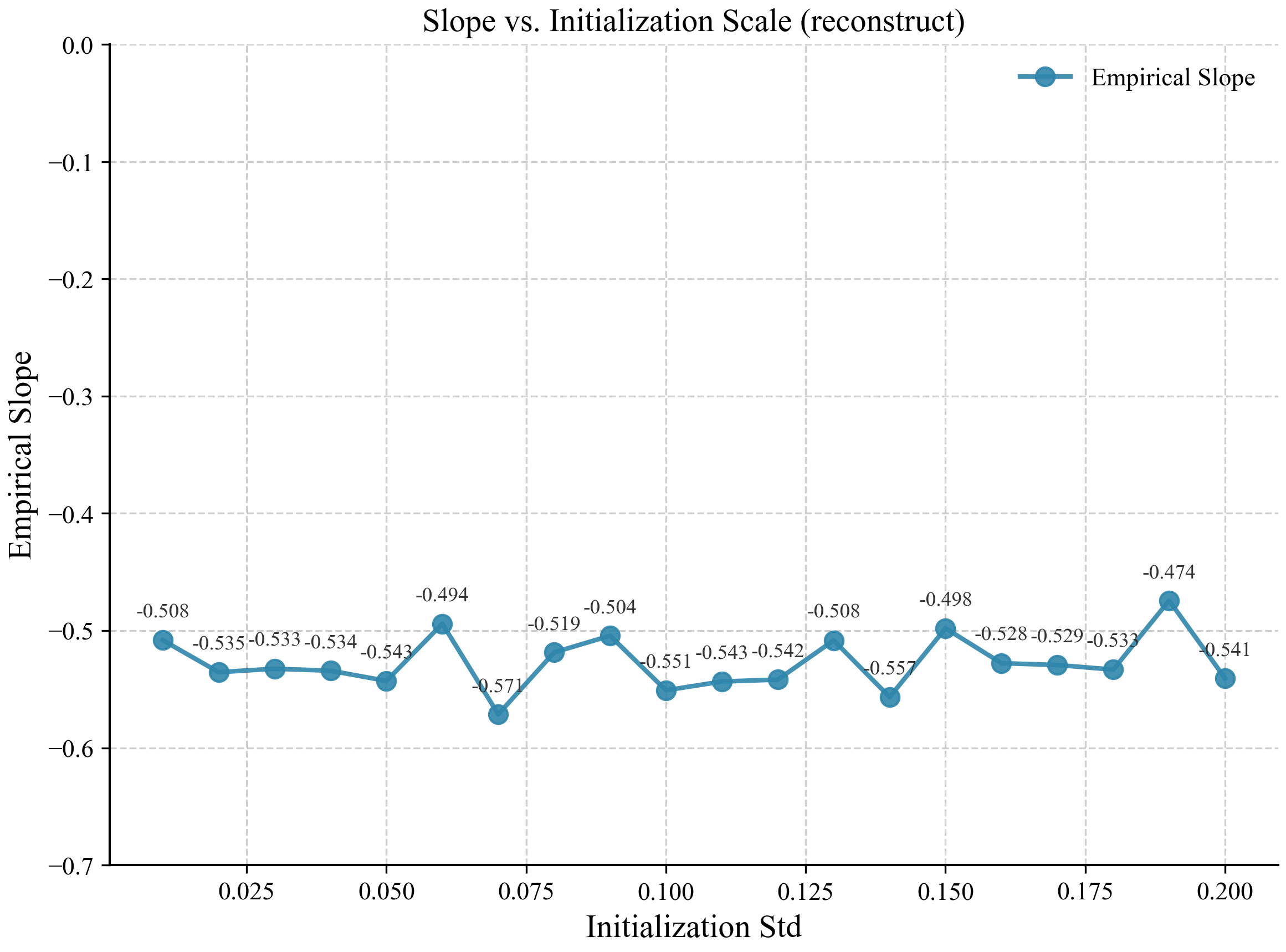
随着初始化 std 增大，empirical 的直线逐渐偏离理论预测的直线。那如果我们把 empirical slope 关于 std 的曲线画出来会是什么样子？结果如下

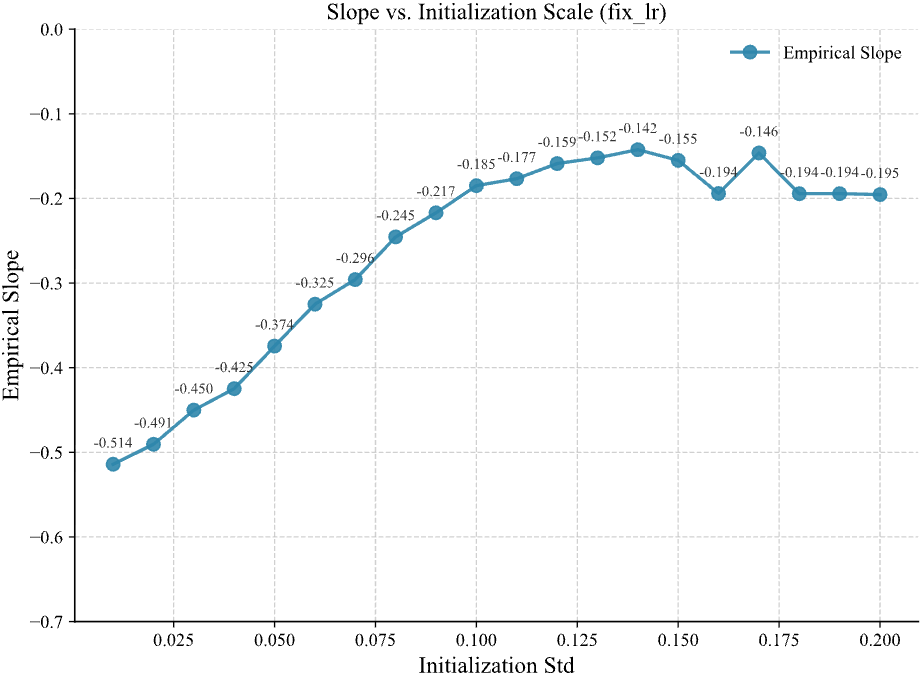
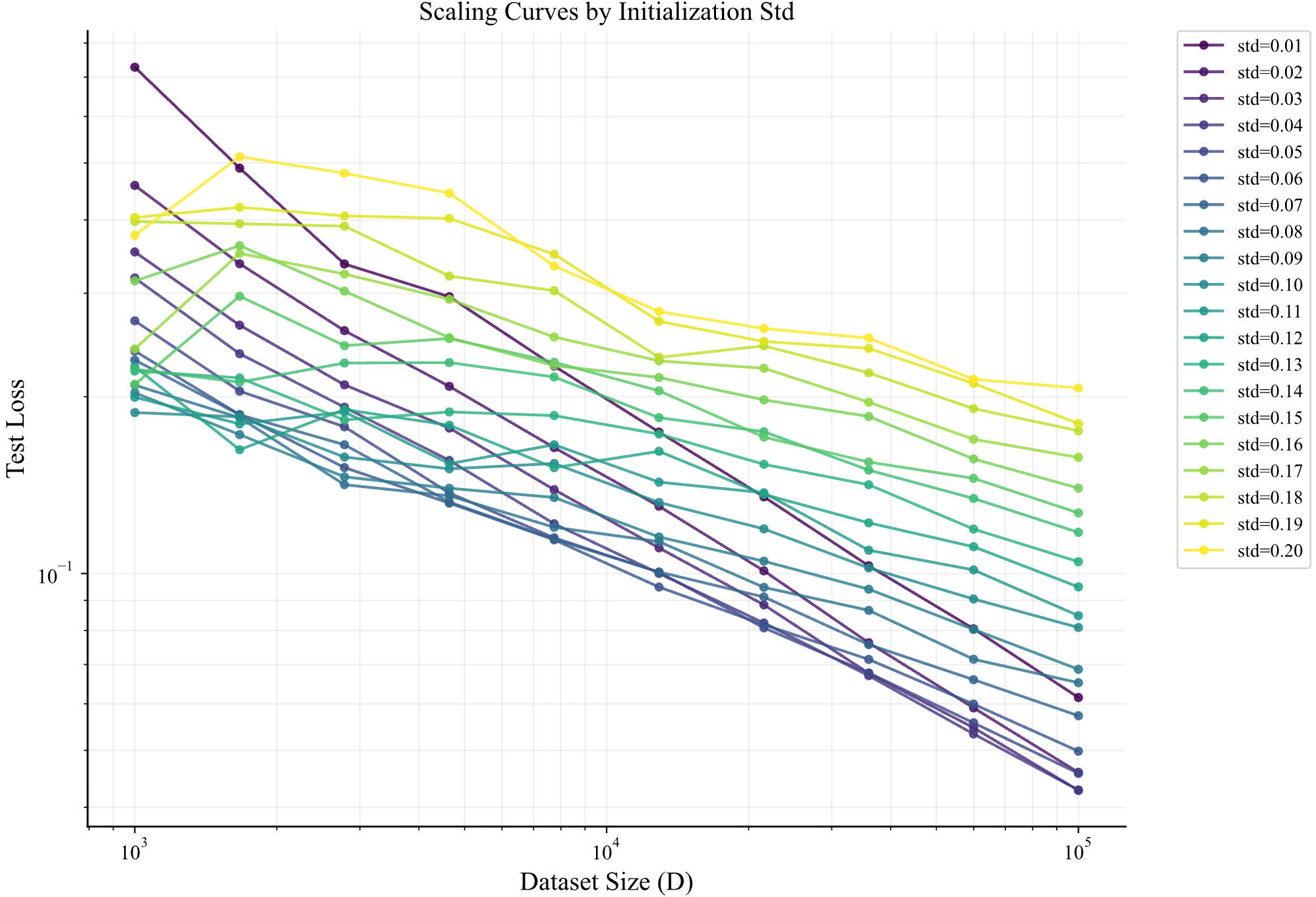
这个结果就很有趣了，可能的原因有很多，比如 std 太大导致模型进入了 lazy learning regime；或者 std 增大带来了优化过程的不稳定（这一种可能原因有待商榷，因为我测试了不同 epoch 数，结果是上图中的曲线仍能够稳定复现）。但我们可以先不考虑其诱因，先来考虑如何对齐不同初始化大小下的 data scaling 曲线。

前提定义

我们考虑一个两层 ReLU 网络，其前向计算写成 $g(W_1,W_2;x)=W_2\phi(W_1 x)$，其中$\phi=\mathrm{ReLU}$，且满足正齐次性：对任意 $c>0$,

\[\phi(cu)=c\,\phi(u).\]

输入 $x\in\mathbb R^K$ 被设为 One-hot 或归一化向量且满足 $\lVert x\rVert^2=1$，隐藏层先得到预激活 $h=W_1 x$ 再经 ReLU 得到激活值 $a=\phi(h)=\mathrm{ReLU}(h)$，最终输出 $y=W_2 a\in\mathbb R^K$，而隐藏层宽度记为 $N$。权重矩阵 $W_1,W_2$ 均按 $\mathcal N(0,\sigma^2)$ 独立同分布地初始化。对于任意元素均值为 $0$、方差为 $\sigma^2$ 的矩阵 $A\in\mathbb R^{d_{\mathrm{out}}\times d_{\mathrm{in}}}$，其 Frobenius 范数的期望平方满足 $\mathbb E[\lVert A\rVert_F^2]=d_{\mathrm{out}}\cdot d_{\mathrm{in}}\cdot\sigma^2$，因而量级上 $\lVert A\rVert_F \propto \sigma$。

尝试 1 (失败)

固定学习率 lr 的情况下，增大初始化 std，虽然绝对步长不变，但是相对于$\lVert W\rVert_F$的步长就小了，过小的权重更新量会导致模型落入 lazy learning regime。从这点出发我们需要计算 相对更新比率 R：

\[\mathcal{R} = \frac{\lVert\Delta W\rVert_F}{\lVert W\rVert_F} = \frac{\lVert\eta \cdot \nabla W\rVert_F}{\lVert W\rVert_F}\]

这是分母部分，非常直接。 对于第二层权重 $W_2 \in \mathbb{R}^{K \times N}$：

\[\mathbb{E}[\lVert W_2\rVert_F^2] = K \cdot N \cdot \sigma^2\]

取均方根作为量级估计：

\[\lVert W_2\rVert_F \approx \sqrt{KN} \cdot \sigma \propto \sigma\]

下面我们估计$\lVert\nabla W_2\rVert_F$。预激活 $h$ 的每个元素 $h_j$ 服从 $\mathcal{N}(0,\sigma^2$。$\text{Var}(h_j) = \sigma^2$。对于激活层输出 a：$a_j = \text{ReLU}(h_j)$。由于 ReLU 将负半轴置零，二阶矩减半：

\[\mathbb{E}[a_j^2] = \frac{1}{2} \mathbb{E}[h_j^2] = \frac{1}{2} \sigma^2\]

则激活层的向量范数 $\lVert a\rVert^2 = \sum_{j=1}^N a_j^2$ 的期望为：

\[\mathbb{E}[\lVert a\rVert^2] = N \cdot \frac{1}{2}\sigma^2 \implies \lVert a\rVert \propto \sqrt{N}\sigma\]

---

对于第二层输出 y：$y_k = \sum_{j=1}^N W_{2, kj} a_j$。假设 $W_2$ 与 $a$ 独立，且 $\mathbb{E}[W_2]=0$。则

\[\text{Var}(y_k) = \sum_{j=1}^N \text{Var}(W_{2, kj} a_j) = \sum_{j=1}^N \mathbb{E}[W_{2, kj}^2] \mathbb{E}[a_j^2]\]

代入已知项：

\[\text{Var}(y_k) = N \cdot (\sigma^2) \cdot (\frac{1}{2}\sigma^2) = \frac{N}{2} \sigma^4\]

则$\lVert y\rVert \approx \sqrt{\frac{N}{2}} \sigma^2 \propto \sqrt{N} \sigma^2$

---

损失函数 $L = \frac{1}{2} \lVert y - t\rVert^2$。梯度公式为：

\[\nabla_{W_2} L = (y - t) \cdot a^T.\]

当 $\sigma$ 较大时，初始输出 $\lVert y\rVert$ 远大于目标 $\lVert t\rVert$（在我们的 setting 里是 One-hot，量级为 1）。因此，误差项 $\epsilon = y - t \approx y$。现在计算梯度矩阵 $\nabla_{W_2} L$ 的范数：

\[\lVert\nabla_{W_2} L\rVert_F = \lVert(y - t) a^T\rVert_F = \lVert y - t\rVert_2 \cdot \lVert a\rVert_2.\]

代入步骤 2 的结果，$\lVert y - t\rVert \approx \lVert y\rVert \propto \sqrt{N} \sigma^2$，$\lVert a\rVert \propto \sqrt{N} \sigma$。相乘得到梯度量级：

\[\lVert\nabla W_2\rVert_F \approx (\sqrt{N} \sigma^2) \cdot (\sqrt{N} \sigma) = N \sigma^3.\]

---

现在我们将上述结果代入相对更新率公式：

\[\mathcal{R} = \frac{\lVert\Delta W_2\rVert_F}{\lVert W_2\rVert_F} = \frac{\eta \lVert\nabla W_2\rVert_F}{\lVert W_2\rVert_F}\]

代入量级关系：

\[\mathcal{R} \approx \frac{\eta \cdot (N \sigma^3)}{\sqrt{KN} \cdot \sigma}.\]

化简（忽略常数 $K$）：

\[\mathcal{R} \propto \frac{\eta \sigma^3}{\sigma} = \eta \sqrt{N} \sigma^2.\]

为了保持相对更新量恒定，我们需要 $\mathcal{R} = \text{Constant}$，即：

\[\eta \sigma^2 = C \implies \eta \propto \frac{1}{\sqrt{N} \sigma^2}.\]

由于在我们的实验里，$N$是固定的，只改变初始化 std 于是只需要 $\eta \propto \frac{1}{\sigma^2}$. 于是我立刻在代码里实现了这一个调整。结果如下

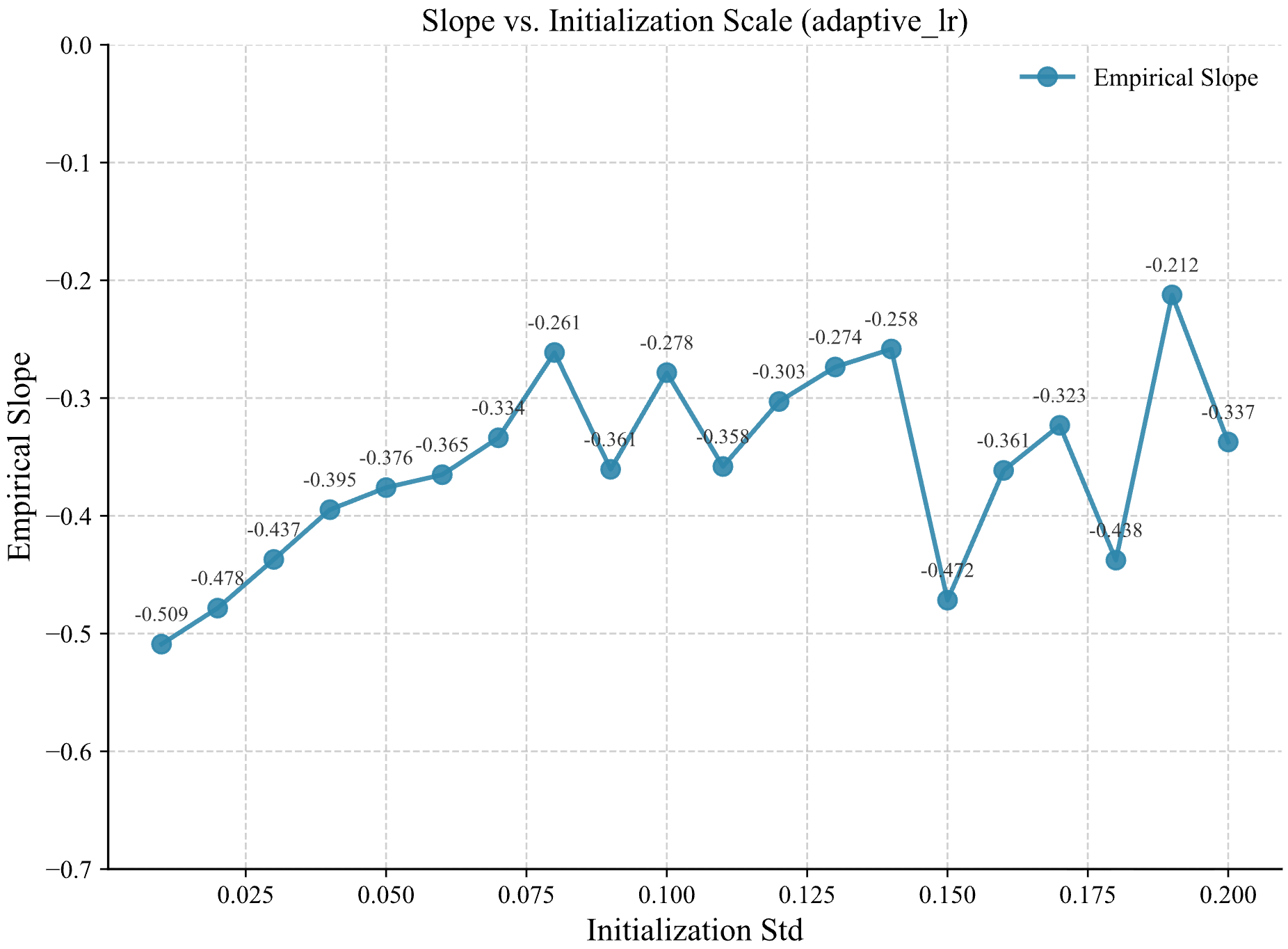
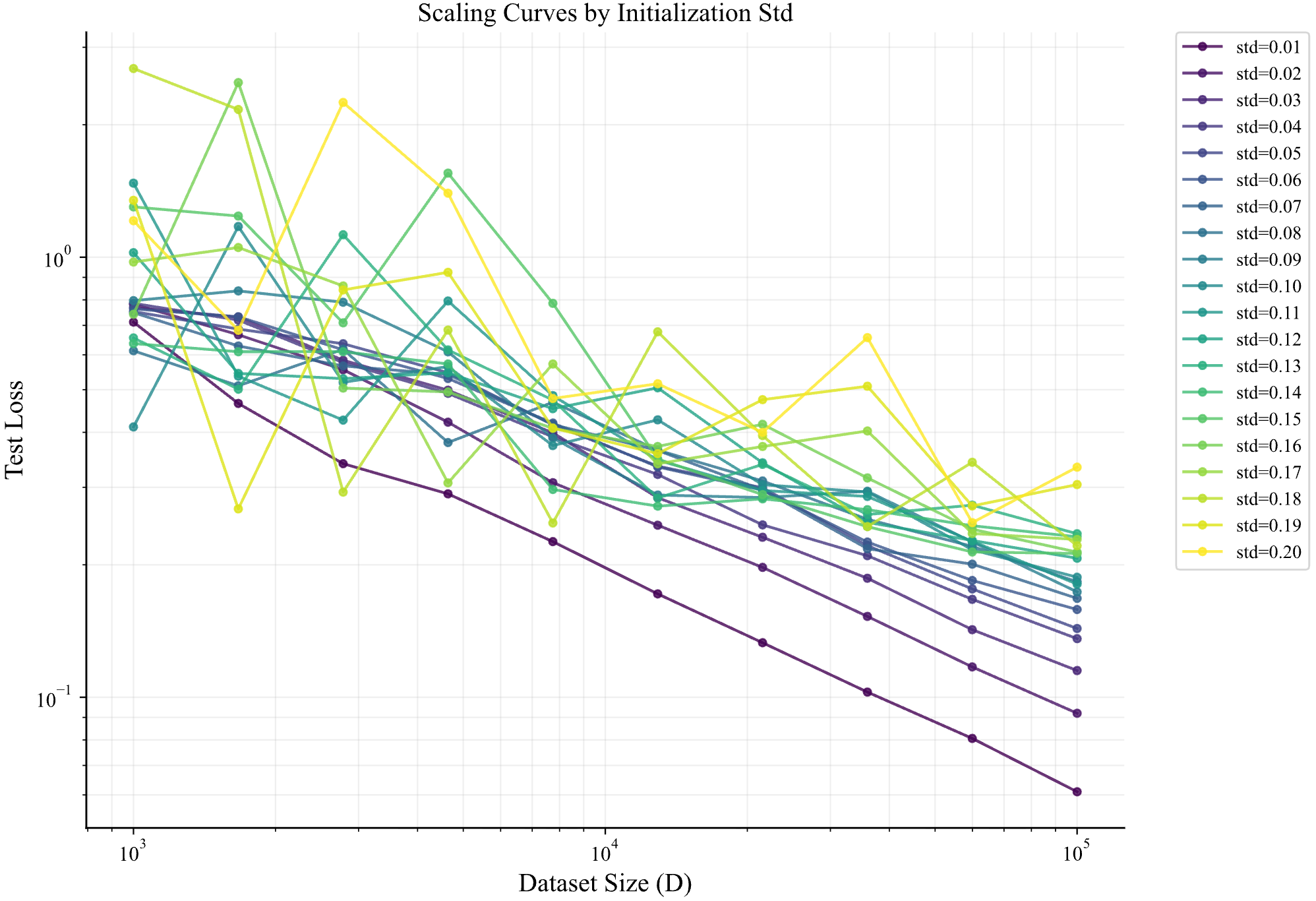
我们放在同一图里对比一下：

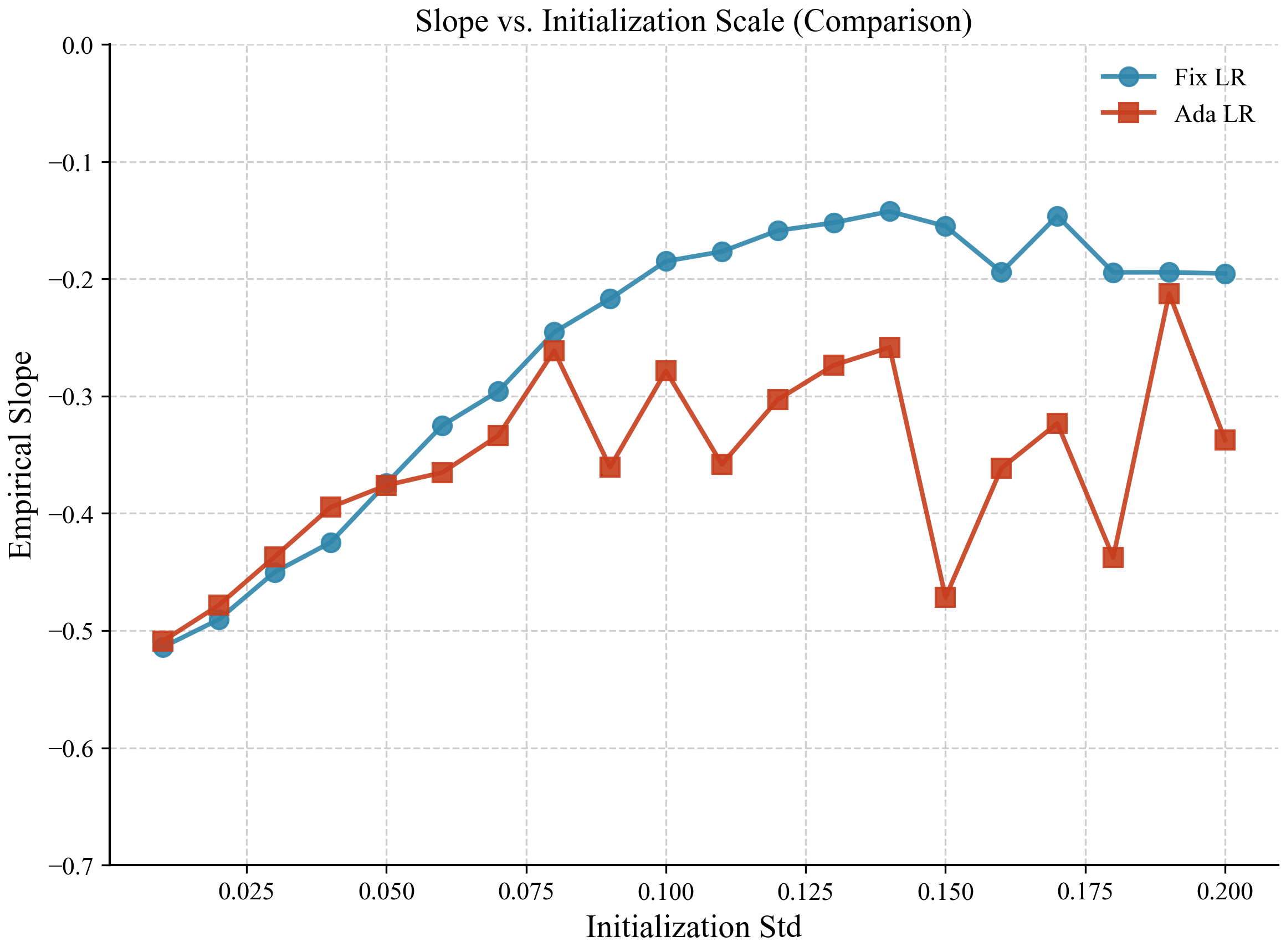
可以看见，自适应学习率 $\eta \propto \frac{1}{\sigma^2}$ 确实缓解了一点初始化 std 对 scaling 曲线 empirical slope 的影响。但在初始化 std 较小时，仍难以缓解。我认为原因可能是 \(\lVert\nabla W_2\rVert_F \approx N \sigma^3\)这个近似成立的前提需要较大的 $\sigma$（详见前文推导），所以在初始化 std 较小的情况下，$\eta \propto \frac{1}{\sigma^2}$未必正确。

尝试 1 失败的原因（probably）

除了近似成立的区间，我们还可以这样分析。在我们论文里的设定下，把参数写成 $W=\sigma U$ 后，模型对应的风险是

\[\mathcal L_\sigma(U)=\sum_{k=1}^K p_k\underbrace{\big(\sigma^2 g(U;e_k)-1\big)^2}_{q_k}.\]

注意目标 “1” 固定不随 $\sigma$ 缩放（绝大部分情况下，真实标签也不随 $\sigma$ 缩放），这一步已经破坏了尺度不变性。

对 $W$ 做梯度下降

\[W^{t+1}=W^t-\eta \nabla_W \mathcal L(W^t),\]

换成 $U^t=W^t/\sigma$，可以推得精确更新式

\[U^{t+1} =U^t-2\eta\sum_{k=1}^K p_k\big(\sigma^2 g(U^t;e_k)-1\big)\,\nabla_U g(U^t;e_k). \tag{★}\]

这里面有个不可消掉的因子：

\[(\sigma^2 g(U^t;e_k)-1).\]

它依赖于当前 $U^t$ 和样本 $k$，不是全局常数。总的来说，不可能用一个标量 $\eta(\sigma)$ 来做到对齐效果。$\eta\propto 1/\sigma^2$ 在某些 regime 会稍微好一点（因为它对齐了某个主要尺度，比如 NTK 主项）。但它不可能把所有 $\sigma$ 的训练变成同一个问题，仍会有系统性漂移与不稳定。

尝试 2 (成功)

到底要怎样才能对齐所有 $\sigma$ 的data scaling 曲线？

为了把原来输出自动带 $\sigma^2$的缩放在 forward 中抵消掉，我们令

\[f_\sigma(x;W)=\frac{1}{\sigma^2}W_2\phi(W_1x), \qquad W_i\sim\mathcal N(0,\sigma^2),\]

并令学习率 $\eta_\sigma\propto\sigma^2$。

若写 $W=\sigma U$，此时就有

\[\begin{aligned} f_\sigma(x;\sigma U) &=\frac1{\sigma^2}(\sigma U_2)\phi((\sigma U_1)x)\\ &=\frac1{\sigma^2}(\sigma U_2)\cdot(\sigma\phi(U_1x))\\ &=U_2\phi(U_1x)=:f_1(x;U). \end{aligned}\]

右边完全不含 $\sigma$。

令目标函数

\[\mathcal J_\sigma(W)=\sum_{k=1}^K p_k\big(f_\sigma(e_k;W)-1\big)^2, \quad f_\sigma(x;W)=\sigma^{-2}W_2\phi(W_1x).\]

令 $U=W/\sigma$。则易得：

1. 目标函数本身不含 $\sigma$：

\[\mathcal J_\sigma(\sigma U)=\mathcal J_1(U).\]

1. 梯度缩放（链式法则）：

\[\nabla_W\mathcal J_\sigma(\sigma U)=\frac1\sigma \nabla_U\mathcal J_1(U).\]

1. 梯度下降轨迹：

定义 $U^t:=W^t/\sigma$，则

\[U^{t+1}=\frac{W^{t+1}}{\sigma} =\frac{W^t}{\sigma}-\frac{\eta_\sigma}{\sigma}\nabla_W\mathcal J_\sigma(W^t) =U^t-\frac{\eta_\sigma}{\sigma}\nabla_W\mathcal J_\sigma(\sigma U^t).\]

代入 $\nabla_W\mathcal J_\sigma(\sigma U^t)=\frac{1}{\sigma}\nabla_U\mathcal J_1(U^t)$，得

\[U^{t+1} =U^t-\frac{\eta_\sigma}{\sigma}\cdot\frac{1}{\sigma}\nabla_U\mathcal J_1(U^t) =U^t-\frac{\eta_\sigma}{\sigma^2}\nabla_U\mathcal J_1(U^t).\]

这个时候关键的地方来了，我们要取 $\eta_\sigma=\sigma^2\eta_0$，才能得到

\[U^{t+1}=U^t-\eta_0\nabla_U\mathcal J_1(U^t),\]

推广到 momentum SGD，也同样严格等价。

综上，我们需要设定

\[f_\sigma(x;W_1,W_2)\;:=\;\frac{1}{\sigma^2}\,W_2\,\phi(W_1x).\]

初始化：

\[W_1^{(0)},W_2^{(0)} \stackrel{\text{i.i.d.}}{\sim}\mathcal N(0,\sigma^2).\]

学习率选择：

\[\eta_\sigma = \sigma^2 \eta_0.\]

这样才能够让不同初始化 std 下的 loss-$D$ 曲线对齐。下面是实验结果

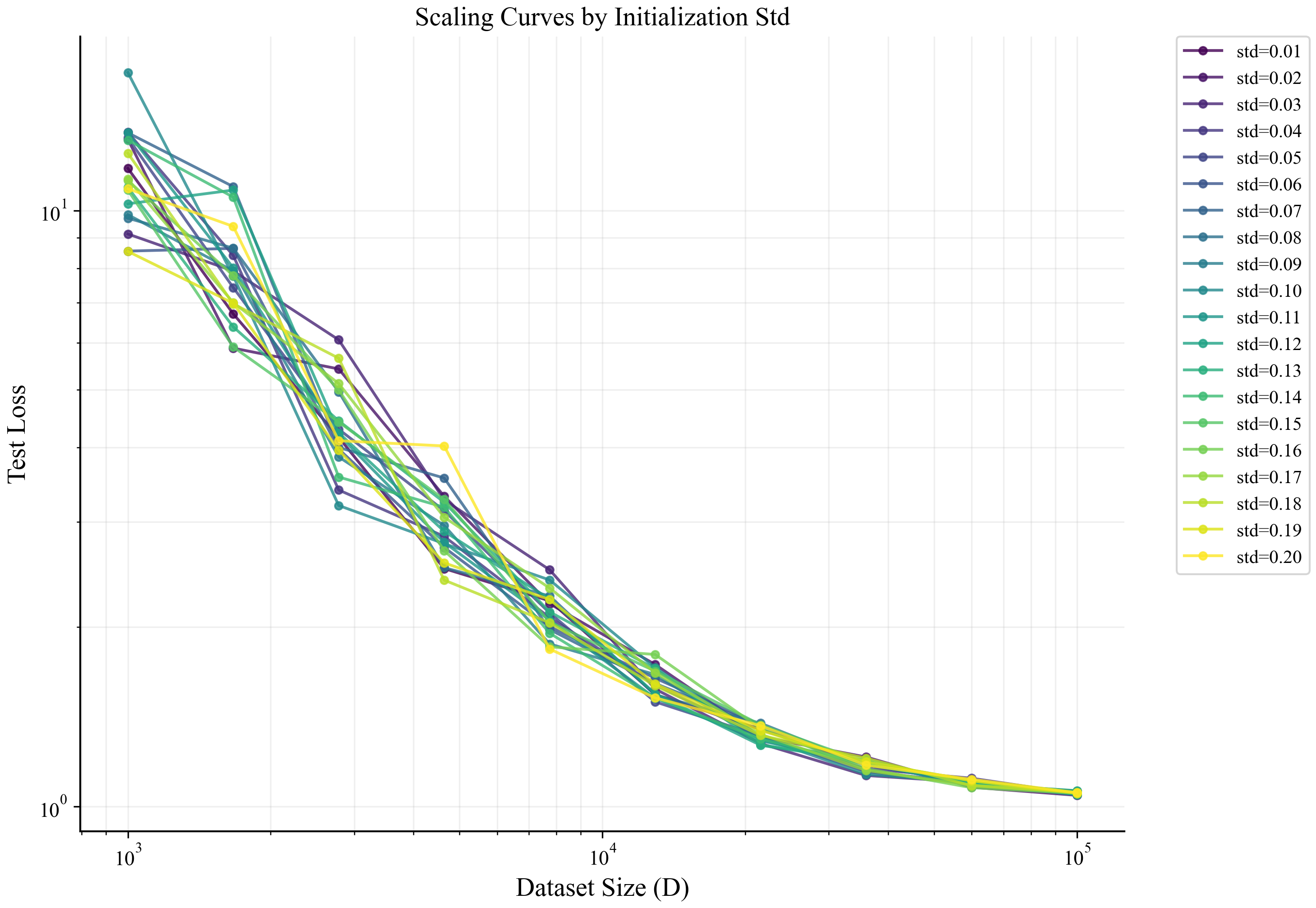
这个结果可以很容易推广到多层relu网络。设网络满足：

• $h_0=x$
• $h_\ell=\phi(W_\ell h_{\ell-1})$, $\ell=1,\dots,K-1$
• $f(x;W)=W_K h_{K-1}$

并且初始化时所有层 $W_\ell\sim \mathcal N(0,\sigma^2)$。定义归一化后的模型输出：

\[\tilde f_\sigma(x;W)=\frac{1}{\sigma^K}f(x;W).\]

只要选：

\[\eta_\sigma=\sigma^2 \eta_0\]

就可以同时对齐 forward 和 backward 过程。