从 Gated DeltaNet 到 Kaczmarz
很多linear attention,都可以被看成在维护一个 Key 到 Value 的线性映射矩阵 $S_t$。Gated DeltaNet [1] 的特别之处在于:它不直接写入 $K_t^\top V_t$,而是写入预测残差,并用门控控制遗忘与写入强度。
1. Gated DeltaNet 的更新公式
在时刻 $t$,给定行向量形式的 $K_t \in \mathbb{R}^{1\times d_k}$ 和 $V_t \in \mathbb{R}^{1\times d_v}$,以及记忆矩阵 $S_t \in \mathbb{R}^{d_k\times d_v}$。
Gated DeltaNet 的核心递推公式为:
\[\begin{aligned} e_t &= V_t - K_t S_{t-1} \\ S_t &= \alpha_t S_{t-1} + \beta_t K_t^\top e_t \end{aligned}\]其中门控通常由输入 $X$ 产生:
- $\beta_t = \sigma(\mathrm{Linear}_\beta(X))$ 代表写入强度。
- $\alpha_t \in (0,1]$ 是遗忘/衰减系数,用来控制对旧记忆 $S_{t-1}$ 的保留比例。
2. Online learning 视角
我们可以把 $S$ 视作多输出线性回归的权重:$\hat V_t = K_t S$。对单样本的在线岭回归损失函数为:
\[\ell_t(S)=\frac12\|V_t-K_tS\|_F^2+\frac{\lambda_t}{2}\|S\|_F^2\]其梯度为:
\[\nabla_S\ell_t(S)=-K_t^\top e_t+\lambda_t S\]如果做一步梯度下降(学习率为 $\beta_t$):
\[\begin{aligned} S_t &=S_{t-1}-\beta_t\nabla_S\ell_t(S_{t-1})\\ &=(1-\beta_t\lambda_t)S_{t-1}+\beta_tK_t^\top(V_t-K_tS_{t-1}) \end{aligned}\]对比 Gated DeltaNet 的形式:
\[S_t=\alpha_tS_{t-1}+\beta_tK_t^\top(V_t-K_tS_{t-1})\]我们可以得到精确的对应关系:$\alpha_t = 1-\beta_t\lambda_t$。而在实现中,通常用 $\alpha_t=\exp(g_t)$ 来保证数值稳定性。
3. 引入 Kaczmarz 算法
在约束视角下,SGD 不是唯一的优化方法。当我们更强调满足约束的几何意义时,可以把每个 token 看成一个线性约束 $K_tS = V_t$。
Kaczmarz 的一步更新可以定义为:在满足当前约束的集合里,找一个离旧解最近的 $S$,即最小改动投影:
\[S_t=\arg\min_S\frac12\|S-S_{t-1}\|_F^2\quad\text{s.t.}\quad K_tS=V_t\]我们可以通过拉格朗日乘子法来求解。构造拉格朗日函数:
\[\mathcal{L}(S,\lambda)=\frac12\|S-S_{t-1}\|_F^2+\lambda(K_tS-V_t)\]对 $S$ 求导并令其为零:
\[\nabla_S\mathcal{L}=(S-S_{t-1})+K_t^\top\lambda=0 \Rightarrow S=S_{t-1}-K_t^\top\lambda\]将 $S$ 代回约束条件 $K_tS=V_t$:
\[K_t(S_{t-1}-K_t^\top\lambda)=V_t \Rightarrow K_tS_{t-1}-\|K_t\|_2^2\lambda=V_t\]解得:
\[\lambda=-\frac{V_t-K_tS_{t-1}}{\|K_t\|_2^2} = -\frac{e_t}{\|K_t\|_2^2}\]因此得到 Kaczmarz 递推公式:
\[\boxed{ S_t=S_{t-1}+\frac{1}{\|K_t\|_2^2}\,K_t^\top e_t }\]4. 几何解释
Kaczmarz 算法具有明确的几何意义:
- 投影意义:Kaczmarz 的更新步骤将 $S_{t-1}$ 投影到超平面 ${S:K_tS=V_t}$ 上。
- 误差消除:当使用硬投影时,更新后的 $S_t$ 满足当前约束,即 $K_tS_t=V_t$。
- 最优步长:它可视作最优步长的一步梯度法。若对瞬时平方误差沿梯度方向进行精确线搜索,最优步长为 $1/|K_t|^2$。
- QK Norm 视角:这个归一化因子也解释了如今 Attention / Linear Attention 在实现层面会加的一个 trick——QK Norm,我们在这里就显式地引入了它。
5. 推广到不一致约束
在现实情况中,约束往往是不一致的或带有噪声的,不存在一个 $S$ 能同时满足所有约束。硬投影可能会导致模型抖动或过拟合当前样本。
因此常用 Relaxed Kaczmarz(或 Damped Kaczmarz),在分子引入松弛系数 $\rho_t$,并在分母加数值稳定项 $\varepsilon$:
\[\boxed{ S_t = S_{t-1} + \frac{\rho_t}{\|K_t\|_2^2+\varepsilon}\,K_t^\top\bigl(V_t-K_tS_{t-1}\bigr) }\]该更新公式满足以下性质:
\[K_tS_t=(1-\rho_t)K_tS_{t-1}+\rho_tV_t\]即新的预测值是旧预测值与目标值之间的线性插值。
若结合 Gated DeltaNet 的遗忘机制,可采用先遗忘后投影的更新方式:
\[\tilde S_{t-1}=\alpha_tS_{t-1},\qquad S_t=\tilde S_{t-1}+\frac{\rho_t}{\|K_t\|^2+\varepsilon}K_t^\top\bigl(V_t-K_t\tilde S_{t-1}\bigr)\]6. 与 Longhorn 的联系
Longhorn [2] 采用了更平滑的更新策略,将硬约束投影替换为近端目标优化:
\[S_t=\arg\min_S\frac12\|S-S_{t-1}\|_F^2+\frac{\gamma_t}{2}\|V_t-K_tS\|_F^2\]其显式解为:
\[\boxed{ S_t = S_{t-1} + \frac{\gamma_t}{1+\gamma_t\|K_t\|_2^2} K_t^\top\bigl(V_t-K_tS_{t-1}\bigr) }\]这个系数可以重写为:
\[\frac{\gamma_t}{1+\gamma_t\|K_t\|^2} = \frac{1}{\|K_t\|^2+\frac{1}{\gamma_t}}\]只需令 $\varepsilon_t = 1/\gamma_t$,这表明 Longhorn 类似于 Kaczmarz。
7. 方法对比表
| 方法 | 状态更新 | 有效步长 |
|---|---|---|
| Gated DeltaNet | $S_t=\alpha_tS_{t-1}+\beta_tK_t^\top e_t$ | $\beta_t$ |
| Kaczmarz | $S_t=S_{t-1}+\frac{1}{|K_t|^2}K_t^\top e_t$ | $\frac{1}{|K_t|^2}$ |
| Relaxed Kaczmarz | $S_t=S_{t-1}+\frac{\rho_t}{|K_t|^2+\varepsilon}K_t^\top e_t$ | $\frac{\rho_t}{|K_t|^2+\varepsilon}$ |
| Longhorn / Prox | $S_t=S_{t-1}+\frac{\gamma_t}{1+\gamma_t|K_t|^2}K_t^\top e_t$ | $\frac{1}{|K_t|^2+1/\gamma_t}$ |
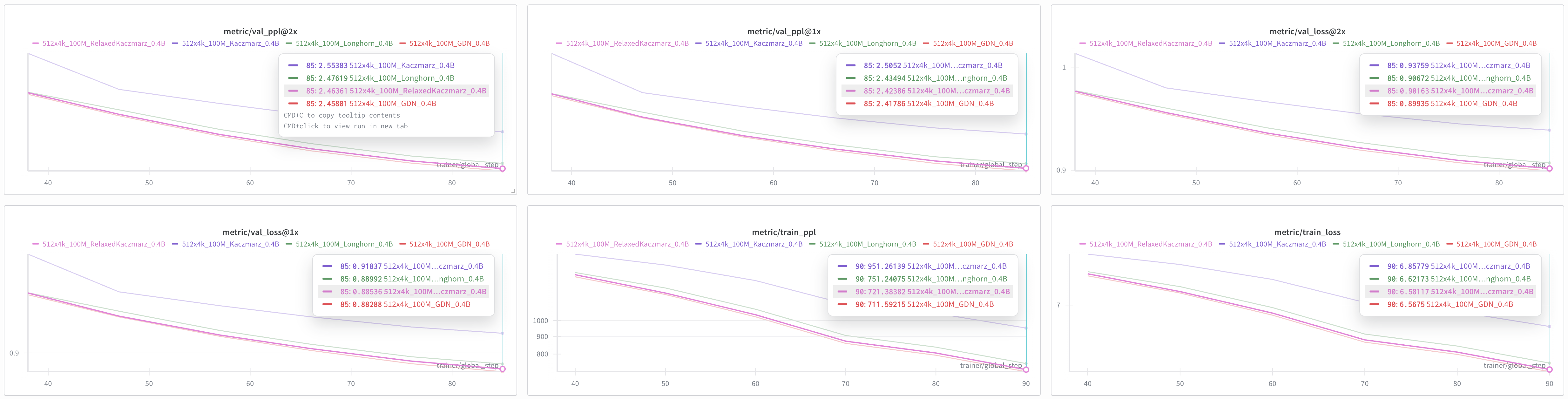
8. 实验
我们在 SlimPajama 数据集上训练了 1 亿个 token,并在验证集上绘制了困惑度(ppl)与 Loss 随 token horizon 变化的曲线。图中 @1x 与 @2x 分别对应序列长度 2048 与 4096 的评估结果。若 Longhorn 可视为 Kaczmarz 的某种形式,则 Relaxed Kaczmarz 理应更优,实验亦证实了这一点。
参考文献
[1] Yang, S., Kautz, J., & Hatamizadeh, A. (2025). Gated Delta Networks: Improving Mamba2 with Delta Rule. arXiv preprint arXiv:2412.06464.
[2] Liu, B., Wang, R., Wu, L., Feng, Y., Stone, P., & Liu, Q. (2024). Longhorn: State Space Models are Amortized Online Learners. arXiv preprint arXiv:2407.14207.
引用
如果您需要引用本文,请参考:
@article{zou2026kaczmarz,
title={从 Gated DeltaNet 到 Kaczmarz},
author={Zou, Jiaxuan},
journal={Jiaxuan's Blog},
year={2026},
url={https://jiaxuanzou0714.github.io/blog/2026/kaczmarz/}
}
Enjoy Reading This Article?
Here are some more articles you might like to read next: